Table of Contents
Tutorial on hyperbolic surfaces
A hyperbolic surface with cusps is a topological surface together with a hyperbolic structure of finite area. polymake can deal with hyperbolic surfaces in view of Penners coordinates of the decorated Teichmüller space (lambda lengths). These allow to pick a hyperbolic surface by choosing a triangulation of the surface along with one positive parameter for each edge.
The secondary fan of a hyperbolic surface stratifies the space of weight vectors (horocyclic decorations) according to which Delaunay triangulations are induced by the Epstein-Penner convex hull construction.
For each point on the surface, there is a secondary polyhedron whose normal fan is the secondary fan.
This tutorial shows how to deal with secondary fans and secondary polyhedra of hyperbolic surfaces.
Construction of hyperbolic surfaces
To define a hyperbolic surface we need to specify (a) a triangulation and (b) Penner coordinates.
(a)
The triangulation is obtained by specifying the DCEL_DATA as an Array<Array<Int>>.
This constructs a doubly connected edge list as follows:
Each row of DCEL_DATA reads { (2i).head , (2i+1).head , (2i).next , (2i+1).next }.
In general, for each edge i of the triangulation there are two half edges 2i and 2i+1, one for each orientation.
(b)
The PENNER_COORDINATES assign a positive rational number to each edge of the triangulation, ordered in the same sense as prescribed by the DCEL_DATA.
Example 1: hyperbolic sphere with three cusps
> application 'fan'; > application 'topaz'; > $S3 = new Array<Array<Int>>([[1,0,2,5],[2,1,4,1],[0,2,0,3]]); > $s = new HyperbolicSurface(DCEL_DATA=>$S3,PENNER_COORDINATES=>[1,1,1]);
In this example the doubly connected edge list looks like this:
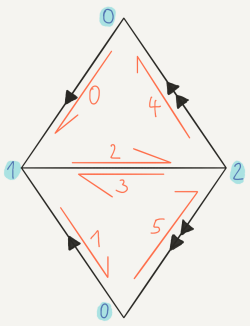
The secondary fan
The secondary fan of the hyperbolic sphere from above can now be computed as follows.
> $f = $s->SECONDARY_FAN; > $f->properties; type: PolyhedralFan<Rational> MAXIMAL_CONES {0 1 2} {0 1 3} {1 2 4} {0 2 5} RAYS 0 1 1 1 0 1 1 1 0 0 0 1 1 0 0 0 1 0 > $f->VISUAL;
> $s->properties; name: s type: HyperbolicSurface DCEL_DATA 1 0 2 5 2 1 4 1 0 2 0 3 FLIP_WORDS {} {0} {1} {2} PENNER_COORDINATES 1 1 1 SECONDARY_FAN type: PolyhedralFan<Rational>
The FLIP_WORDS indicate how to obtain the Delaunay triangulations.
The k-th flip word is a list of integers (the indices of the edges) that describe which edge flips produce the k-th Delaunay triangulation. Note that the k-th Delaunay triangulation also corresponds to the k-th maximal cone of the SECONDARY_FAN.
GKZ vectors & secondary polyhedra
In order to compute GKZ_VECTORS or a secondary_polyhedron of a hyperbolic surface one needs to additionally specify a SPECIAL_POINT on the surface. This is done by choosing two rational numbers.
Continuing with the above example, lets look at the following.
> $s = new HyperbolicSurface(DCEL_DATA=>$S3,PENNER_COORDINATES=>[1,1,1],SPECIAL_POINT=>[1,0]);
Now we may compute an approximation of the GKZ_VECTORS of the surface.
The approximation depends on a parameter depth that restricts the depth of the (covering) triangles that are summed over in the definition of the GKZ vectors.
> print $s->GKZ_VECTORS(3); 1 33346854621/25672050625 33346854621/25672050625 19782163/27238250 1 2361/3250 3955357/5447650 33346854621/25672050625 1 10549213550005124385885122/6365327663846199230365625 11433978/13287625 30327974429709/105771923977850 1 11433978/13287625 10549213550005124385885122/6365327663846199230365625 30327974429709/105771923977850
The secondary polyhedron can be computed similarly using the function secondary_polyhedron.
> $p = secondary_polyhedron($s,10); > $p->properties; name: p type: Polytope<Float> CONE_AMBIENT_DIM 4 VERTICES 1 1.315301353 1.315301353 0.7316378744 1 0.7316489581 0.7316267908 1.315301353 1 1.752046187 0.8750928112 0.2910011302 1 0.8750928112 1.752046187 0.2910011302 0 -1 0 0 0 0 -1 0 0 0 0 -1 VERTICES_IN_FACETS {0 1 3 4} {0 1 2 5} {0 2 3 6} {1 4 5} {2 5 6} {3 4 6} > $p->VISUAL(FacetColor=>'255 180 80');
We may look at the GKZ domes of the individual Delaunay triangulations.
> $d0 = $s->gkz_dome(0,5); > $d0->VISUAL(FacetColor=>'80 180 255');
> $d1 = $s->gkz_dome(1,5); > $d1->VISUAL(FacetColor=>'80 180 255');
Example 2: a hyperbolic torus with three cusps
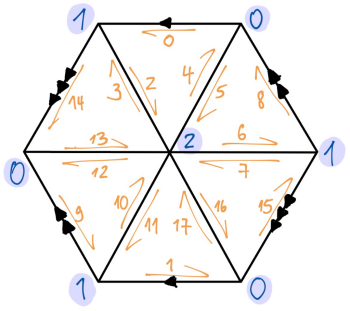
> $T3 = new Array<Array<Int>>([[1,0,2,17],[2,1,4,14],[0,2,0,6],[1,2,8,16],[0,1,5,10],[2,1,12,1],[0,2,9,3],[0,1,13,7],[0,2,15,11]]); > $s = new HyperbolicSurface(DCEL_DATA=>$T3, PENNER_COORDINATES=>[2,1,1,1,1,1,1,1,1], SPECIAL_POINT=>[1,0]);
> $f = $s->SECONDARY_FAN; > $f->VISUAL;
> $s->properties; name: s type: HyperbolicSurface DCEL_DATA 1 0 2 17 2 1 4 14 0 2 0 6 1 2 8 16 0 1 5 10 2 1 12 1 0 2 9 3 0 1 13 7 0 2 15 11 FLIP_WORDS {0} {} {0 3} {0 4 7} {0 6} {3} {6} {0 3 1 5} {0 6 2 8} {3 1 5} {6 2 8} {0 3 1 5 0 1} {0 6 2 8 0 2} PENNER_COORDINATES 2 1 1 1 1 1 1 1 1 SECONDARY_FAN type: PolyhedralFan<Rational> SPECIAL_POINT 1 0 > $p = secondary_polyhedron($s,7); > $p->VISUAL(FacetColor=>'255 180 80');
> $d0 = $s->gkz_dome(0,5); > $d0->VISUAL(FacetColor=>'80 180 255');
> $s = new HyperbolicSurface(DCEL_DATA=>$T3, PENNER_COORDINATES=>[2,1,1,1,1,1,1,1,1], SPECIAL_POINT=>[new Rational(1.5196714),new Rational(-0.5773503)]); > $p = secondary_polyhedron($s,7); > $p->VISUAL(FacetColor=>'255 180 80');
> $d0 = $s->gkz_dome(0,5); > $d0->VISUAL(FacetColor=>'80 180 255');
More examples can be studied via the following:
> # a torus with two cusps (6 edges) > $T2 = new Array<Array<Int>>([[0,0,6,5],[0,0,1,10],[0,0,8,2],[1,0,11,4],[1,0,7,3],[1,0,9,0]]); > > # a sphere with four cusps (6 edges) > $S4 = new Array<Array<Int>>([[1,0,2,6],[2,1,4,9],[0,2,0,11],[3,0,8,5],[1,3,1,10],[2,3,3,7]]); > > # a double torus with two cusps (12 edges) > $DT2 = new Array<Array<Int>>([[0,0,8,10],[0,0,12,14],[0,0,16,18],[0,0,20,22],[1,0,23,2],[1,0,13,3],[1,0,9,1],[1,0,11,4],[1,0,15,6],[1,0,21,7],[1,0,17,5],[1,0,19,0]]);
To study 4-dim. secondary fans the following method is useful. It intersects the secondary fan with the 3-dim. standard simplex.
> sub norm($){ > my $B = new Matrix(shift); > for (my $i = 0; $i < $B->rows(); ++$i) { > my $sum = 0; > for (my $j = 1; $j < $B->cols(); ++$j) { > $sum = $sum + $B->elem($i,$j); > } > $x = 1/$sum; > $B->row($i) = $x * $B->row($i); > } > return $B; > } > $s = new HyperbolicSurface(DCEL_DATA=>$S4,PENNER_COORDINATES=>[1,1,1,1,1,1],SPECIAL_POINT=>[1,0]); > $f = $s->SECONDARY_FAN; > $v = ones_vector | $f->RAYS; > $a = norm($v); > $b = $a->minor(All,~[0]); > $c = ones_vector | $b; > $q = new fan::PolyhedralComplex(POINTS=>$c,INPUT_POLYTOPES=>rows($f->MAXIMAL_CONES)); > $pro = fan::project_full($q); > $pro->VISUAL;